Uji t & Anova
t-TEST & ANOVA
Uji t (t-test) merupakan prosedur pengujian parametrik rata-rata dua kelompok data, baik untuk kelompok data terkait maupun dua kelompok bebas. Untuk jumlah data yang sedikit maka perlu dilakukan uji normalitas untuk memenuhi syarat dari sebaran datanya.
Umumnya pada uji t dua kelompok bebas, yang perlu diperhatikan selain normalitas data juga kehomogenan varian. Kehomogenan data digunakan untuk menentukan jenis persamaan uji t yang akan digunakan.
A. Persamaan berikut ini digunakan jika variansi data antara dua kelompok sampel sama.
Dengan perhitungan derajat bebas:
Umumnya pada uji t dua kelompok bebas, yang perlu diperhatikan selain normalitas data juga kehomogenan varian. Kehomogenan data digunakan untuk menentukan jenis persamaan uji t yang akan digunakan.
A. Persamaan berikut ini digunakan jika variansi data antara dua kelompok sampel sama.
Dengan perhitungan derajat bebas:
B. Persamaan berikut ini digunakan jika variansi data antara dua kelompok sampel berbeda.
Dengan perhitungan derajat bebas (degree of freedom)
Terlihat perbedaan antara kedua persamaan pada perhitungan Standar Error of Mean/pembagi selisih rata-rata. Selain itu perbedaan juga terletak pada perhitungan derajat bebas kedua persamaan itersebut. Umumnya pada software statistik kedua perhitungan itersebut ditanpilkan sehingga hal yang penting untuk memilih perhitungan mana yang akan digunakan terlebih dulu dilihat apakah hasil perhitungan nilai variansi kedua kelompok sampel berbeda atau sama.
Anova Merupakan prosedur pengujian parametrik rata-rata lebih dari dua kelompok data. Pada pengujian Anova selain data harus terdistribusi normal, variansi antar perlakuan harus homogen. Sebelum pengujian Anova dilakukan, maka perlu dilakukan explorasi data untuk melihat apakah kedua asumsi dipenuhi. Jika asumsi kehomogenan varian tidak terpenuhi dapat diatasi dengan mentransformasi data yang ada, prinsipnya adalah rentang data yang besar diusahakan menjadi mengecil, salah satu dengan tranformasi Logaritma. Untuk data yang tidak terdistribusi normal dapat di transormasi dengan beberapa teknik tranformasi seperti Box-Cox Transformation atau Johnson Transformation.
Pada uji Anova umumnya diikuti oleh uji lanjutan berupa uji Turkey (Beda Nilai Jujur), Beda Nilai Terkecil (BNT), Benferoni dll. Penggunaan jenis uji lanjutan didasarkan pada pemenuhan asumsi ke homogenan variansi serta tingkat sensitifitasan dari pengujian.
ARTIKEL TERKAIT APLIKASI UJI:
t-test dengan SPSS (Berikut cth data) ==> Klik disini
UJI ANOVA dengan SPSS (Berikut cth data) ==> Klik disini
UJI ANOVA dan UJI KONTRAS ==> Klik disini
ARTIKEL TERKAIT APLIKASI UJI:
t-test dengan SPSS (Berikut cth data) ==> Klik disini
UJI ANOVA dengan SPSS (Berikut cth data) ==> Klik disini
UJI ANOVA dan UJI KONTRAS ==> Klik disini

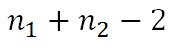



2 komentar:
Terima kasih banyak gan.. atas infonya :)
Cara Download Video Youtube
GOOD
Posting Komentar